Navigation: Toolkit

Marteloio Basics

The Venetian technique for course plotting and recovery was called the marteloio. Nobody knows where this word came from or exactly what it means, but it generally refers to a series of rules applied to the contents of a pre-calculated trigonometric table.

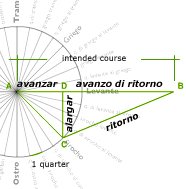
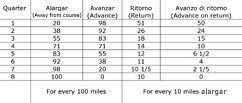
Michael considered the table so important he wrote it out twice in his discussion of the marteloio technique. Below are the contents of Michael's table and a diagram that makes it easier to understand:

Click to enlarge the diagram
Click to enlarge the marteloio table
The marteloio table

On the diagram, the line AB indicates the intended course of the vessel. AC is the direction the ship is actually headed, for which the navigator wants to calculate a correction. The first column of the table lists the eight quarters of the windrose on which the navigator could be sailing away from AB.

Sailing along a quarter wind, Michael got farther away from his intended course (AB). The second column of the table states the number of miles he would be off course (CD), or alargar, after sailing 100 miles on each of the eight quarter winds.

Even while sailing off course, Michael usually made some headway toward his destination. The third column of the table gives the number of miles advanced (AD), or avanzar, for every 100 miles sailed off course on each of the eight quarters. Naturally, if Michael sailed at 90 degrees (eight quarters), he would have made no advance toward his destination.

When the wind changed, Michael could sail back to his course. The fourth column gives the return distance, or ritorno, he would have to sail (CB) on each quarter for every 10 miles he was off course (alargar). These quarter winds were considered in relation to the intended course, or a line parallel to the intended course.

While sailing back to the intended course, Michael would have made some headway toward his destination. The last column of the table gives us the distance advanced (DB) for every 10 miles off course (avanzo di ritorno).

The values in the marteloio table are based on the trigonometry of right-angle triangles. But Michael did not have to know anything about trigonometry to use it—and there is no trigonometry in the mathematical portion of this manuscript. All he had to do was apply standard rules for a given situation.

See how Michael recovers a course, deals with multiple course changes, or plots a course in advance.