Mathematics: Toolkit
The Rule of Double False Position
The first problem in Michael's manuscript concerns the value of 315 pounds of pepper. After solving the problem using the rule of three and algebra, Michael solves it again using the rule of double false position.
The rule of double false position was an ancient technique for dealing with problems that we would now call linear equations, particularly of the form ax + b = c.
The rule of double false technique was very useful for solving equations at a time when the absence of modern notation made the use of algebra difficult.
Michael's use of double false technique for his pepper calculation is probably overkill, but it shows his genuine interest in math.
In essence, the procedure asks the user to come up with two arbitrary, incorrect solutions for the value of x. The wrong answers are used to get the right answer by following a series of steps.
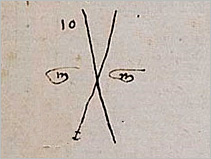
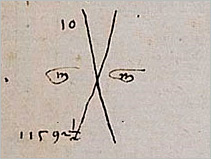
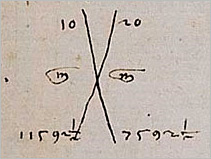
The graphic form of a large X—seen throughout Michael's mathematical text—is used to guide the procedure. To the left and right of the X is the letter m with a line over it; this is the abbreviation of the Venetian word 'men', which means 'minus.'
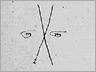
The arbitrary, incorrect solutions are placed at the top of the X. The difference they each make when compared to an expected value is put at the bottom of the X. The numbers are then multiplied, added, and subtracted across the X in a set order, ending in a final division.
-
a) First solution in ducats
Michael begins by guessing that the value of this cargo will be 10 ducats, placing the 10 at the top left of the X.
Then he constructs a statement of the problem that will guide his calculations:
"If
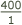 gives me
gives me 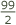 ducats, what will 315 give me?"
ducats, what will 315 give me?"This statement is in the form of the rule of three and Michael's rule was to solve such problems by adding the second and third terms together, dividing by the first. We would write this as:
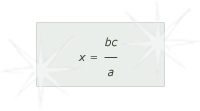
Michael knows the problem can also be expressed as:
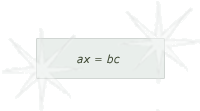
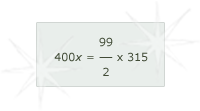
In this case, the equation would be:
-
1] Michael gets his expected value from the right side of the equation.
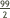 x 315 = 15592
x 315 = 15592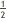
-
2] He inserts his false value for x in the left side of the equation.
400 x 10 = 4000
-
3] He subtracts the false value from his expected value and places the result at the bottom of his big X.
15592
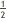 - 4000 = 11592
- 4000 = 11592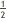
-
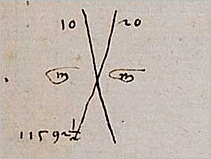
4] Now Michael repeats the procedure with a second wrong guess, namely that the value of his cargo will be 20 ducats. He places 20 at the top right of the big X.
-
5] His expected value is again 15592
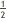 .
. -
6] He inserts his second false value x in the left side of his equation.
400 x 20 = 8000
-
7] He subtracts the false value from his expected value and places the result at the bottom of his big X.
15592
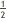 - 8000 = 7592
- 8000 = 7592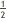
-
8] Now Michael is ready to solve the problem. The first step was to multiply across the big X and combine the results. His first multiplication is:
7592
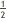 x 10 = 75925
x 10 = 75925
-
9] He then completes his second multiplication across the big X.
11592
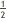 x 20 = 231850
x 20 = 231850
-
10] To combine these products, Michael stated a set of rules about what to do if the differences placed at the bottom of the big X represented numbers more than the expected value (as could happen with an arbitrary solution of more than 50 ducats) or less. In this case, the rule was to was to subtract.
231850 - 75925 = 155925

-
11] Following the same rule, Michael subtracts the differences at the bottom of the big X and notes that this is the divisor (partidor).
11592
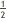 x 7592
x 7592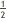 = 4000
= 4000
-
12] Finally, he carries out the galera division.
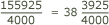

Michael then simply says to carry out the calculations on the remainder to get the amounts in smaller coins, arriving at the same answer as before, namely that his cargo of pepper is worth 38 ducats, 23 denari, and 17
 piccoli.
piccoli.
-
-
b) A second solution in ducats
Michael's first use of double false position was already excessively complicated compared to his use of the rule of three to determine the value of his pepper. But it is typical of Michael that he knew another way to solve the problem using double false position and explained that method, too.
In the first example, Michael was working with an equation whose form we would write as:
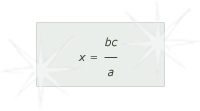
This he transformed into:
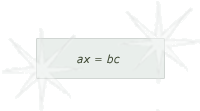
choosing bc to be his expected value.
In his second solution, Michael wants to make the point that another value could be used for the expected value, namely b, the value in ducats, rather than the value in ducats times the number of pounds as he had earlier. We might write this equation as:
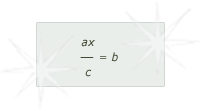
which in numbers of his problem would be:
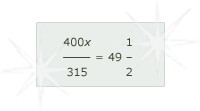
This way Michael doesn't have to make any calculations for his expected value, as he did in the first solution. His expected value is always 49
 .
.-
1] As usual, Michael begins with a statement of the problem:
"If 315 gives 10 of the supposition, what will 400 be?"
-
2] He substitutes false values of 10 and 20 into the equation.
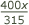
-
3] He writes 10 and 20 at the top of the big X, subtracting the results from his expected value, placing the difference from the expected value at the bottom of the big X.

-
4] He is then ready to multiply across the big X and subtract one product from the other to get a dividend, then subtract one of the numbers at the bottom of the big X to get the divisor.
-
5] All Michael had to do was divide—but he actually doesn't. He merely states that his 315 pounds of pepper will be worth 38 ducats, 23 denari, and
 piccoli.
piccoli.
-
See how Michael solves the problem using the rule of three or algebra.