Michael of Rhodes | Mathematics

Mathematics: Toolkit

Galera Division

To complete the rule of three in his very first math problem, Michael needed to divide 31185 by 800 to find out how much 315 pounds of pepper was worth in ducats. He uses a method of division that was known as the galera, or "galley," method because the triangular form reminded people of galley sails.

This method was standard in the Middle Ages, but looks confusing to us.

The best way to understand Michael's method is to step through it with him.

The galera division in table form

		Here is Michael's galera division as it looks in the manuscript. It's a little confusing because it shows the final result of many earlier steps.
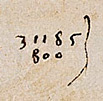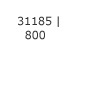		Michael wants to divide 31185 by 800. He starts by writing the divisor (800) below the dividend (31185), then draws a bar to the right. [modern step a]
		Normally, the divisor 800 would be written under the 3 of 31185, and 8 divided into 3. But 8 will not go into 3, so Michael writes the 800 one decimal place to the right. He notes this step by placing a zero over the 3.
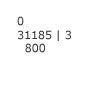		Michael now divides 8 into 31. He knows that it will go three times. He writes the 3 of the quotient beside the bar. [modern step c]
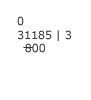		Next, Michael multiples the 3 of the quotient by the 8 of 800 and gets 24. He keeps the 24 in his head and crosses out the 8.
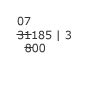		Three times 8 is 24. Michael subtracts the 24 from the 31, crossing out 31. The remainder is 7, which he writes above the divisor, beside the zero. Note that the total remainder is now 7185, but the number is not on one line. [modern step e]
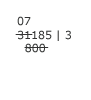		Michael should have multiplied the 3 of the quotient by the remaining digits of the divisor and subtracted them from the dividend. But 3 times zero is zero, so he didn't bother. He should have crossed out the two zeros, but doesn't.
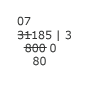		Now Michael writes in the divisor 800, but not on one line. The 8 and zero are written on the lowest line, but the final zero is written on the line above, beside the original divisor.
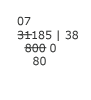		Michael considers how many times 8 will go into 71. The answer is 8. He writes the 8 next to the 3 of the quotient. [modern step h]
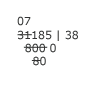		Next, Michael multiplies the 8 in the quotient by the 8 in the divisor. He keeps the 64 in his head and crosses out the 8 in his second divisor.
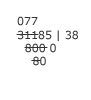		Michael tries to subtract the 4 of 64 from the 1 in the dividend. Since he cannot, he borrows 10 from the first 7 in the remainder, then subtracts 4 from 11 to get 7 again. He writes 7 above the second 1 in the dividend, crossing out the 1 as he does so.
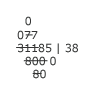		Michael now subtracts the 6 from the first 7. However, he has already borrowed from the 7, so the 7 is really 6. Subtracting 6 from 6 gives zero, which he writes above the 7, crossing out the 7 as he does so. The total remainder is now 785, but the number is not written on one line. [modern step k]
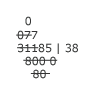		At this point, Michael should have cancelled the remaining zeros in the divisor, but he doesn't bother because he knows 800 will not go into 785. His division is finished. He now knows his 315 pounds of pepper is worth 38 785/800 ducats.